Chapter 7 Segmentation, contour based
Contents:
7.1 Introduction
 |
A segmented image contains collections or groupings of parts of an image that are homogenous in one or more properties:
- intensity or color
- texture (the fine structure in intensity)
- movement (a vector value per pixel)
Primarily, we shall look at the intensity or color, some methods can be extended to texture or movement.
|
We want the groupings to coincide with (parts of) objects or situations in the portrayed scene. The goal is often to divide the entire image into disjoint regions:
Image = k Rk with Ri
Rk with Ri  Rj =
Rj =  for i
for i  j
j
R is a connected region if for each xi and xj in R there is an array {xi,..., xk, xk+1,..., xj } in R where each consecutive pair
(xk, xk+1 ) is connected (4,8 or mixed).
We can try to find both the boundaries of the regions in the image and the regions themselves. Perfect boundaries and regions are redundant, from one you can derive the other and visa versa. The
methods for finding them differ largely in character and suitability for application in particular concrete cases. Boundary- and area-finding techniques can be combined to yield a more reliable
segmented image.
In this chapter "knowledge" becomes important. This can be defined as implicit or explicit boundaries of the probability of a given grouping in an image. This knowledge can be domain dependent,
for example:
this is an image of blocks
there is an airplane to the top left, etc.
It can also be general, physical or heuristical knowledge (properties that hold in the most domains or in the most situations), for example:
most humans have two arms
the maximum velocity or acceleration with movement
preference for the shortest edge between two points
7.2 Edges
7.2.1 Definition
Edges of objects are important for the human visual system, often objects can already be recognized by simply a rough contour. It is difficult to detect the contours of objects directly from an
intensity image. It's a better idea to first transpose the image to one that shows local discontinuities (edges) in the intensity. These discontinuities are often caused by edges of objects.
An edge is a vector that shows a particular position, size and direction of discontinuity. Sometimes only the size is determined. The "direction" of the edge is perpendicular to the "direction" of
the rim of the object, pay clsoe attention to the directions used. An edge can be determined per pixel, but also between connected pixels, the so-called crack edges. Sometimes the position of an edge
is determined with a higher precision than one pixel.
An edge operator is a mathematical function that detects local discontinuities in a limited space. The edge operators can be classified as:
- approximation of the gradient operator
- template matching, check if edge-moulds fit
- fit with parameterized edge-moulds, when more is known about the edges which one wants to find.
 |
These operators, based on parameterized models, cost a lot of calculation time and their benefit is fairly limited; especially if a general edge operator, which can be used without a lot of a
priori information about the image scene, can be used. They can yield more information about the discontinuity than direction and size alone, such as the width of an edge and the size of intensity
transitions to the left and right of the image. We shall not look at this any further.
|
All edge operators have a certain underlying model about the discontinuities which they detect. They yield numbers for the size and direction of the discontinuities, independent of how well that
local piece satisfies the model. This quality "match" is often worked out in the size, but sometimes though in quality or threshold values.
Thresholding is used to remove non-relevant discontinuities (for example, caused by noise or pixels too far from the real edges. Edges can then be linked to each other, called "edge linking" or
"contour following" to find the object's edges.
7.2.2 Points and lines
Isolated pixels are often detected with masks that approximate the Laplacian. These operations are very sensitive to noise. Thresholding yields the pixels that drastically deviate from their
neighborhood.
|-1 -1 -1| | 0 -1 0|
(1/9) |-1 8 -1| or (1/5) |-1 4 -1| R = i=0 8 wipi
8 wipi
|-1 -1 -1| | 0 -1 0| |R| > T
Lines that are one pixel broad can be found using masks:
|-1 -1 -1| |-1 -1 2| |-1 2 -1| | 2 -1 -1|
| 2 2 2| |-1 2 -1| |-1 2 -1| |-1 2 -1|
|-1 -1 -1| | 2 -1 -1| |-1 2 -1| |-1 -1 2|
horizontal +45
vertical -45
Select direction i if: |Ri| > |Rj| for all j, possibly (weighted with |Rk|) averaging values when two directions close to each other yield almost the same
R. Ri indicates the strength of the edge. Thresholding (absolute and relative) is used to remove non-relevant line-elements.
7.2.3 Gradient operators
Using the image function f(x,y) one can determine the vector gradient image:
 (f(x,y) = (
(f(x,y) = ( f/
f/ x,
x,  f/
f/ y )
y )
 = arctan2(
= arctan2(  f/
f/ x ,
x ,  f/
f/ y ) yields the image composed of the directions
y ) yields the image composed of the directions
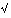 ( (
( ( f/
f/ x)2 + (
x)2 + ( f/
f/ y)2 ) yields the image size, often called the gradient image.
y)2 ) yields the image size, often called the gradient image.
 |
The effect of the first and second order derivative on the edges is shown here (see also fig. 10.7).
|
The gradient operators approximate the mathematical gradient by a discrete calculation of the derivative:
 f/
f/ x = lim
x = lim ->0 { (f(x+
->0 { (f(x+ ) -f(x) ) /
) -f(x) ) /  }
}
The easiest way is:  f/
f/ x = f(x+1,y) - f(x,y) and
x = f(x+1,y) - f(x,y) and  f/
f/ y = f(x,y +1) - f(x,y). This is called "crack edges", they measure the changes over an edge between two pixels.
y = f(x,y +1) - f(x,y). This is called "crack edges", they measure the changes over an edge between two pixels.
Other frequently used ways of determining the derivative are:
|1 0| | 0 1| |-1 -1 -1| |-1 0 1| |-1 -2 -1| |-1 0 1|
|0 -1| |-1 0| | 0 0 0| |-1 0 1| | 0 0 0| |-2 0 2|
| 1 1 1| |-1 0 1| | 1 2 1| |-1 0 1|
Roberts Prewitt
Sobel
|

The original image
|

Edge size is determined using a 3*3 Sobel
|
Prewitt and Sobel take more pixels into account and are thereby less sensitive to noise. Variants with 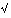 2 are also used a lot. Larger masks, for example 5 by 5, can be used, if at approximation the edges are straight over such a large area. See also fig. 10.10 to 10.12. 2 are also used a lot. Larger masks, for example 5 by 5, can be used, if at approximation the edges are straight over such a large area. See also fig. 10.10 to 10.12.
|
 |
The x and y components of Sobel
Using ideal edge models one can study the functioning of all of these edge operators, variating the edge and distance to the central pixel. Possibly followed by a correction of the direction or
size. The direction and size found can possibly be corrected. Of course, the quality of the edges found is strongly dependent on the signal-noise ratio in the images.
|
|

area
|

with zero-crossing (using XITE)
|
A more general use of the Laplaciaan in finding positions of edges is by detecting the zero-aisles.
|
This coincides with first determining the convolution of the image with the Gaussian function and then taking the Laplacian of it. The result is then thresholded (negative values black, positive
values white) to be able to determine the zero-aisles easily, possibly between pixels. Masks are also used for a better detection of the zero-aisles and directions. The  must be selected appropriately.
must be selected appropriately.
The necessary convolution matrices are large ( 9x9 for  = 1, 43x43 for
= 1, 43x43 for  = 5), but the calculations can be made faster (CVGIP 32,279-290,1985 and CVGIP 48,147-189,1989), because the LOG
(Laplacian or Gaussian) is separable: LOG(x,y) = h12(x,y) + h21(x,y) with h12(x,y) = h1(x)h2(y) and h21(x,y) =h2(x)h1(y). The LOG can also be approximated with a DOG ( difference or Gaussian with
different
= 5), but the calculations can be made faster (CVGIP 32,279-290,1985 and CVGIP 48,147-189,1989), because the LOG
(Laplacian or Gaussian) is separable: LOG(x,y) = h12(x,y) + h21(x,y) with h12(x,y) = h1(x)h2(y) and h21(x,y) =h2(x)h1(y). The LOG can also be approximated with a DOG ( difference or Gaussian with
different  s). There are indications that biological systems also do this.
s). There are indications that biological systems also do this.
In 2-D we want to execute a convolution with the first derivative of a 2-D Gaussian in a direction n perpendicular to the edge:
Gn =  G/
G/ n = n .
n = n .  G with
G with  G = (
G = ( G/
G/ x,
x,  G/
G/ y)
y)
n =  (G
(G Im) / |
Im) / |  (G
(G Im) | (this is true for approximation)
Im) | (this is true for approximation)
 ( Gn
( Gn Im) /
Im) /  n = 0 thus
n = 0 thus  2 (G
2 (G Im) /
Im) /  n2 = 0 (local maximum)
n2 = 0 (local maximum)
In his implementation Canny used simple masks to calculate n and a simple peak-determination with one threshold in the direction of n.
Fleck (IEEE PAMI 14,337-345,1992) improved this (other masks and 3 thresholds) and compared results and real images with modified Marr-Hildreth and Boie-Cox edge determiners. Results are
comparable but differ somewhat in the behavior of undesirable artifacts where the image does not suffice with the underlying model.
Deriche (Int J. Computer Vision 1,167-187,1987) found an I(x) that was 90% better than the derivative of the Gaussian and can also be implemented rapidly. In 2-D the derivatives can be found by
convolution with masks that are separable (13 * and 12 + per pixel).
 |
 |
To the left the direction of the edges. To the right the thinned edges (see chapter 7.3), multiplied by a factor of 2.5. |
7.2.4 Templates
These are often motivated by the Kirsch operator:
S(x) = maxk k-1 k+1 |f(xk)-f(x)| k+1 |f(xk)-f(x)|
 (x) = kmax * 45° (x) = kmax * 45° |
k walks around x : 4 3 2
5 x 1
6 7 8
|
Possible implementations:
|-3 -3 5| |-3 5 5| | 5 5 5| |-3 -3 -3|
|-3 5| |-3 5| |-3 -3| ... |- 3 5|
|-3 -3 5| |-3 -3 -3| |-3 -3 -3| |-3 5 5|
This implementation uses 8 templates, so 8 values are calculated for each pixel in the image. The template with the highest match value defines the edge strength (equal to that match value) and
the edge direction (quantized in steps of 45°).
Using 4 templates, the template with the highest absolute match value defines the strength and direction (just as in 8 discrete directions):
|-1 0 1| | 1 1 1| | 0 1 1| | 1 1 0|
|-1 0 1| | 0 0 0| |-1 0 1| | 1 0 -1|
|-1 0 1| |-1 -1 -1| |-1 -1 0| | 0 -1 -1|
A multitude of such templates (5*5) or (7*7) are possible, however the calculation time increases explosively. The suitability for a certain image depends on the image itself and the prospectives
for use or further processing of the image. A large template blurs small (speaking in terms of space) edges, but is less vulnerable to noise.
Edges with a small magnitude are often caused by noise or small fluctuations without meaning. Thresholding is then used to remove weak edges:
S'(x) = 0 if S(x)  Threshold otherwise
S(x)
Threshold otherwise
S(x)
A better edge detection and thresholding method is that of Frei and Chen which see the edge operator as part of a set of orthogonal functions. The image function around point x0 is
factorized as:
f(x) = k=0 8 (f, hk) hk(x- x0 ) / (hk,
hk) around x0 with (f, hk) = d
8 (f, hk) hk(x- x0 ) / (hk,
hk) around x0 with (f, hk) = d f(x)
hk (x- x0 )
f(x)
hk (x- x0 )
Here (,) is the correlation operation: the projection of the image around x0 on the basis function hk.
An unusable example:
|a b c| |1 0 0| |0 1 0| |0 0 1| |0 0 0|
|d e f| = a |0 0 0| + b |0 0 0| + c |0 0 0| ... + i |0 0 0|
|g h i| |0 0 0| |0 0 0| |0 0 0| |0 0 1|
with for example
|a b c| |0 1 0|
b = |d e f| . |0 0 0|
|g h i| |0 0 0|
Frei and Chen took the following basis functions:
|1 1 1| |-1 -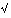 2 -1| | 0 -1
2 -1| | 0 -1 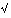 2| | 0 1 0| | 1 -2 1|
2| | 0 1 0| | 1 -2 1|
|1 1 1| | 0 0 0| | 1 0 -1| |-1 0 1| |-2 4 -2|
|1 1 1| | 1 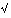 2 1| |-
2 1| |-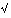 2 1 0| | 0 -1 0| | 1 -2 1|
2 1 0| | 0 -1 0| | 1 -2 1|
|-1 0 1| |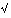 2 -1
0| |-1 0 1| |-2 1 -2|
2 -1
0| |-1 0 1| |-2 1 -2|
|-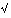 2 0
2 0  2| |-1 0 1| | 0 0 0| | 1 4 1|
2| |-1 0 1| | 0 0 0| | 1 4 1|
|-1 0 1 | | 0 1 - 2| |
1 0 -1| |-2 1 -2|
2| |
1 0 -1| |-2 1 -2|
no
structure gradient ripple line point
Every basis function corresponds to a certain local shape in the image, the corresponding coefficient indicates the strength of it.
Another way of removing noise and double edges is:
S'(x) = S(x) if S(x) is a local maximum, else 0
To determine a local maximum one can look at the 4-connected or 8-connected neighboring pixels.
7.3 Edge thinning
Even after thresholding or determining a local maximum, gradient methods often result in contours that are more than one pixel broad and having noisy edges. A high threshold (even after
determining the local maximum) thins contours but eliminates vague contours. There are also problems in places where contours come together. Often a different thinning step is used to minimize the
amount of edge pixels without losing contours.
A simple way of thinning is comparing the pixel strength in the gradient direction (perpendicular to the edge) of each edge pixel to its neighboring pixels. An edge not having the maximal strength
is removed. The direction can be taken in steps of 45°, or average values of edge strengths can be used. Problems often arise when boundaries come together: (î : an arrow pointing upwards,
/: arrow pointing to the top right))
pixels direction magnitude thinned edges
0 0 0 0 0 0 0
0 0 0 0 0 0 0 î î î î î 5 4 3 3 3 0 0 0 + +
2 2 1 1 1 1 1 î î î î î 6 5 4 3 3 + + + + +
2 2 2 1 1 1 1 / / î î / 1 3 3 2 1 0 0 0 0 0
2 2 2 2 2 1 1 / î î î 0 1 2 3 3 0 0 0 + +
2 2 2 2 2 2 2 î î 0 0 0 1 2 0 0 0 0 0
2 2 2 2 2 2 2
Lacroix (IEEE PAMI 19,803-810,1988) determines a LBE (likelihood of being a edge) per pixel. Every pixel has two counters: v (visited) and m (maximum). While scanning the image a 3x1 window is
placed over every pixel in the gradient direction. Every pixel in the window gets the value v incremented by 1, only the pixel(s) with the highest value get the value w incremented by 1. After the
scan LBE becomes LBE = m / v :
v m LBE
2 2 2 2 2 0 0 0 2 2 0 0 0 1 1
1 2 3 2 1 1 2 3 2 1 1 1 1 1 1
2 2 4 3 3 0 0 2 0 0 0 0 1/2 0 0
1 1 2 4 2 0 0 0 4 2 0 0 0 1 1
1 0 1 2 2 0 0 0 0 0 0 0 0 0 0
LBEs of 0 are obviously not edges, so LBEs of 1 are then used to start new contours and lower LBEs are only used to continue with already existing contours. Naturally, during contour-following,
different thresholds can be applied to the edge strength.
Edge relaxation is an iterative method to improve edge values by adjusting them depending on the measured edges in the neighborhood. The confidence we have in detecting an edge becomes dependent
on the strengths of the edges in the neighborhood:
0 Initial confidence C0(e) e.g.: magnitude / maximal magnitude.
1 k=1
2 for each edge, use the confidences of the edges in the neighorhood to calculate a type.
3 calculate Ck(e)= function { type, Ck-1(e) }
4 evaluate convergency criteria (for example all the confidences are near to 0 or 1, or the maximal number of iterations has been reached); stop or ( k++ ) and go back
to 2.
 |
For example:
A "crack edge" has three neighbors to the left and right. First determine the number of strong neighbors. This can easily be done using a threshold method or a more complicated method. The type of
edge then becomes (i,j): (the number of strong neighbors to the left, respectively to the right). The confidences are then changed depending on the type:
|
Ck(e) = Ck-1(e) + C for type (1,1) (1,2) (1,3) and reversibly
C for type (1,1) (1,2) (1,3) and reversibly
Ck-1(e) -  C for type
(0,0) (0,2) (0,3) and reversibly
C for type
(0,0) (0,2) (0,3) and reversibly
Ck-1(e) all other cases
 C is an appropriately chosen constant, and of course the Cks are kept in the interval
[0,1].
C is an appropriately chosen constant, and of course the Cks are kept in the interval
[0,1].
7.4 Linking and contour following
7.4.1 Linking
 |
In the picture on the left we have tried to detect the straight lines (see also figure 10.16).
The method can be adjusted (how?) to find circles (see the picture on the right).
|
 |
Lacroix based her contour follower on that of Kunt:
Start with a non-marked (located on the contour) LBE=1 pixel and follow a contour perpendicular to the gradient direction (so in the direction of the contour) first to the left and afterwards to the
right.
|
determine the neighbors in the directions p(erpendicular), u(p) and d(own)
max = maximum ( LBE(p), LBE(u), LBE(d) )
If LBE(p) = max: (same direction)
p == marked: stop
p becomes the next point
if LBE(u) and/or LBE(d) = 1 : set LBE(u and/or d) = 0.9
Otherwise if 1 of u or d has LBE=max : (change in direction)
marked: stop
becomes the next point
Otherwise: both have LBE=max: (junction)
both are marked: stop
1 not marked: becomes the next point
both not marked: choose the one with the best fitting gradient, set the LBE of the other to 1.
When nothing about the shape of the contour is known, but regions can easily be recognized (for example in a binary image) we can use "blob finding" methods:
1) walk through the image until an regional pixel (a 1) is found
2) if it is a regional pixel: turn to the left and take one step; otherwise turn to the right and take one step
3) go to 2) except if the initial pixel has been reached
This algorithm can be extended to:
- generate a row of boundary pixels without duplicates
- find the contour of 8-connected figures
- find multiple objects in the image
- reconstruct an object out of its contour points.
 |
This method can also be extended to gray level images. Assume that a contour has been followed to a point xi. Go to the xj, connected to xi in the direction
perpendicular to the gradient of xi. If the magnitude of the gradient is large enough, assume that xj lies on the contour. Otherwise determine if xj lies inside or
outside of the region, by for example looking at the average gray level around xi. Then determine a new search position xk.
|
7.4.2 Searching with a given location
 |
Imagine that we roughly know the edge of a region. Use the given edge to explore and search (at a constant distance and perpendicular to the edge) for a pixel with the maximal edge value. If
enough edge points have been found, then an analytical curve (for example in a low order polynomial) can be fit; this then becomes the new representation of the boundary.
|
The given edge can be known for example in a previous image or series of images, from a map with a satellite image or from a previously taken satellite photo of the same region. The given edge can
also be known analytically, e.g. straight lines in an image recording of blocks or circular shapes in an image of a bubble chamber.
 |
In a bubble chamber charged elementary particles (protons, electrons, muons, etc.) generate boiling bubbles in an over-heated liquid, for example liquid hydrogen. Incoming particles can interact
with the proton of the hydrogen nucleus resulting in charged and non-charged particles. The bubble chamber is located in a magnetic field, the path of a particle is therefore a helix.
|
The interactions are photographed, with the bubbles of a particle almost forming circles in the image. Simultaneously a threesome of recordings from different directions are made. From
measurements of the bubble paths in each "view" and knowledge of the recording apparatus (position, magnification and lens distortions, intermediate materials: air, glass wall, liquid, etc.) the
spatial paths of the particles can be calculated.
At the end of the 50s, large computer systems (main-frames) were used for calculations but the measurements were made manually. During the 60s the development started for computer driven
measurement apparatuses. Using the hardware and software methods on a small row of bubbles, element traces were determined by precisely measuring the position and orientation. This was one of the
first examples of mini-computer used to control an apparatus, and not solely for doing calculations.
 |
People thought it would be simple to automatically find all the interactions and measure paths on photos, because it is so easy for people to do! That quickly proved to be wrong, the human visual
system has pattern recognition capabilities that are not (yet) possible with digital computer methods. That is why the measuring software was given certain initial information: the position of the
vertex and one or two start elements on each trail.
|
From a starting element the first path element is found. Together with the vertex this defines a circle, from which the region of the next path element is determined. Newly found elements make it
possible to determine the circle more precisely (and even deviations thereof) so that the trace can be followed and even in difficult regions such as: many crossing traces or scratches on the film,
under-exposure of light, liquid turbulences, etc.
Besides the human operator who checked the measurements and gave the software new starting points when problems arose, reliance was on the aid of computer graphics apparatuses and software. In
such a manner, a semi-automatic interactive measuring system is created by combining the capabilities of humans and computers to get the desired measurements. Improvement in the measurment and
recognition software lead to quicker, more automatic systems. For example with the so-called Vertex Guidance software (the subject of my thesis) only some outgoing particles and a rough approximation
of the position of the vertex is known initially. Then, in circles around the vertex, starting points are searched for to follow. Bubble chambers are not used anymore but the development methods are
still of importance in modern electronic detection apparatuses for determining the paths of particles.
7.4.3 Hough methods
 |
These methods are based on the method of P. Hough (US patent 1962) for detecting lines. Points in a parameter space are calculated from the points or edge values in the image, such that the
structures being looked for easily form recognizable structures in the parameter space.
|
Look at all the possible lines which can go through an image point (s,t): t = m s + c. The parameters of all these lines form a straight line in the parameter space spanned by m and c. The point
where the two lines intersect in the parameter space defines the line that goes through the points (s,t) and (u,v). Both m and c can attain any value from -  to +
to +  , what
gives problems. In this aspect, a better way to parameterize the line is:
, what
gives problems. In this aspect, a better way to parameterize the line is:
x cos  + y sin
+ y sin  = r
= r
The  's : from -90° to +90° and r:
's : from -90° to +90° and r:  1/2 D , where D is the diagonal of the image.
1/2 D , where D is the diagonal of the image.
We have the following Hough algorithm to determine lines (where several points or edges lies on) in an image:
- initialize A(rd, d)=0 for all rd and
d)=0 for all rd and d, make the accumulator matrix discrete
d, make the accumulator matrix discrete
- for every point (x,y) having a value > Threshold :
calculate the r and  for all the possible
lines through (x,y), make the value discrete to rd and
for all the possible
lines through (x,y), make the value discrete to rd and d, then set
A(rd,
d, then set
A(rd, d) := A(rd,
d) := A(rd, d) + 1 for all rd and
d) + 1 for all rd and d
d
- the local maximum in A yields the parameters of lines where a lot of points lie on. The corresponding edges and end points of the lines must be determined.
 |

Accumulator matrix
of the Hough Line
(multiplied by a factor
5) See also
[fig. 10.20]
|
In the top left the input points are shown, thinned edges with a value larger than 20. Under that the lines found using XITE Hough Line are shown, with the update-limit set to 0.09. In the bottom
picture the input points are shown that are located on the line that was found.
A lot of points in the accumulator matrix must be attained per point in the original image. In the edge image we also know the  for every (x,y), so we can fill in less points in A: for every (x,y), so we can fill in less points in A:
- initialize A(rd, d)=0 for all rd and d)=0 for all rd and d, a discrete accumulator matrix d, a discrete accumulator matrix
- for every point (x,y) with edge G(x,y) > Threshold and angle  : :
m = tg (  - -  /2 ) and c = y - m x /2 ) and c = y - m x
calculate r and  , make the value discrete
until rd and , make the value discrete
until rd and d d
then set A(rd, d) :=
A(rd, d) :=
A(rd, d) + 1 d) + 1
- the local maximum in A yield the parameters of lines on which many edges lie.
Because  is very inaccurate (sometimes only measured in steps of 45°, sometimes more precise) in
practice we must take more values of (r, is very inaccurate (sometimes only measured in steps of 45°, sometimes more precise) in
practice we must take more values of (r, ) for every edge and placed in A. The errors of the edge detection in
(x,y) can also be taken into A. Finding the local maximum in A is a problem on its own, but there are well-known algorithms to deal with that. ) for every edge and placed in A. The errors of the edge detection in
(x,y) can also be taken into A. Finding the local maximum in A is a problem on its own, but there are well-known algorithms to deal with that.
|
 |
 |
However, if we look at two edges in an image then the number of possible (a,b,r) values strongly decrease. The local maximum in the parameter space are then simpler and easier to find. With n edge
points (stronger than the threshold) in the image, there are n(n-1)/2 pairs to be viewed. Boundaries on r and testing on the  s can restrict the number of (a,b,r) values to be calculated.
s can restrict the number of (a,b,r) values to be calculated.
In general, any work done in the parameter space (calculating and tracking down the local maximum) can be replaced by work in the image space.
For every edge (x,y, ) of sufficient strength, we can then calculate several possible (xc,yc) values and
increment the corresponding A(xc,yc). Here we must pay attention to the inaccuracy in (x,y,
) of sufficient strength, we can then calculate several possible (xc,yc) values and
increment the corresponding A(xc,yc). Here we must pay attention to the inaccuracy in (x,y, ).
).
When the scaling factor S and orientation  of the object are not known, the xc and yc must be
calculated for every edge (x,y,
of the object are not known, the xc and yc must be
calculated for every edge (x,y, ) for every r(
) for every r( ) and for all discrete S and
) and for all discrete S and  :
:
xc = x + r( ) S cos ( a(
) S cos ( a( ) +
) +  ) A( xc,yc,S,
) A( xc,yc,S, ) a 4-D matrix
) a 4-D matrix
yc = y + r( ) S sin ( a(
) S sin ( a( ) +
) +  )
)
Over the last years the Hough methods have been of much interest because of the development of efficient data structures to save fairly empty A matrixes and to find the local maximum in it.
7.4.4 Graph methods
A graph is a set of nodes {ni} and arches between the nodes {ni,nj}, possibly with a weight or cost factor. For example, make an arch from pixel xi to
xj if:
- xj is one of the three 8-connected pixels in the direction of  i ( here the direction of the edge)
i ( here the direction of the edge)
- G(xi) > T and G(xj) > T (only the strong edges)
-  (xi) -
(xi) -  (xj) <
(xj) <  /2 (roughly the same direction)
/2 (roughly the same direction)

Assume that we:
- want to find a path from xa (start node) to xb (goal node)
- we have a method for finding the successor nodes (as explained above)
- have an evaluation function f(xj) which is an estimation of the cost of the optimal path from xa to xb through xj.
Then we can use a heuristical search algorithm (the A* algorithm of Nilsson), starting with node xa:
1) expand the current node, place the successors on a list (OPEN) with pointers to the current node.
2) if OPEN is empty: failed
3) retrieve from OPEN the xi with the minimal f(xi):
4) if xi = xb : found, trace back to reconstruct the optimal path
5) make xi the current node and go to 1)
The evaluation function f is often expressed as: f (xi) = s( xa -> xi ) + h( xi -> xb )
if h = 0 :"minimum cost" search
if h(xi) > the actual minimal cost from xi to xb: then the path with the minimal cost can be missed.
The evaluation functions can also contain:
-edge strength maxx s(x) - s(xi) or equality: |sav - s(xi) |
-arching | ( xi ) -
( xi ) -  ( xj ) |
( xj ) |
-distance to a roughly known boundary: dist( xi , Boundary)
-distance to the goal: dist( xi , xb )
Finding boundaries in an image, without a known goal node, can be done as follows:
1) take the strongest edge which has not yet been viewed
2) follow it in a forward direction until there are no successor nodes left over, take the path with the smallest f
3) follow it in the backwards direction
4) go to 1, use every edge only once
Afterwards the small boundaries are removed, double boundaries are brought back to single boundaries and the holes are filled, see [fig. 10.25]
The heuristic search algorithm has the disadvantage that it has to maintain the set of current paths, which can become extremely large. Some alternative methods are:
-Tree pruning: do not look at the paths with a high cost per length unit. This can take place when the number of alternative top nodes has become too large.
-Depth-first: continue with the last expanded node ( OPEN is then structured as a stack)
-Branch and Bound: determine the maximal cost of a path, possibly dependent on its length. Partial paths with a high cost can then be stopped. This boundary can be known or determined by actually
generating a path.
-Least maximum cost: for every path only take the arch with the maximal cost as an estimation of f. This is similar to finding a mountain pass with the lowest altitude. The advantage is that f does
not increase with the length and thus good paths can be followed for a while.
Updated on March the 4th 2003 by Theo Schouten.
