IMC010: Type Theory and Coq

Teachers

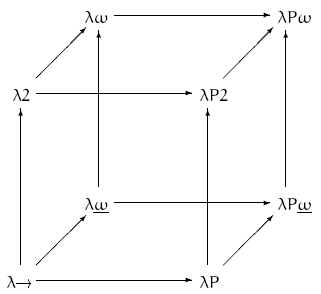
Structure of the course

The course consists of six elements:

1. Lectures on using type theory

Freek will use the first five weeks to teach:

Femke van Raamsdonk, Logical Verification Course Notes

using the schedule:

7 September	introduction & propositional logic	chapter 1
17 September	simple type theory & inductive types	chapters 2 & 3
24 September	predicate logic & dependent types	chapters 4 & 6
1 October	second-order logic & polymorphic types	chapters 7 & 8
8 October	program extraction & inhabitation	chapters 5 & 9

2. Coq practicum

There will be a Coq practicum corresponding to Femke's course notes. For this you need to install Coq and download a

zip file with the practicum files

The completed files need to be handed in in Brightspace. Finishing this practicum is obligatory to be able to pass the course, but there will not be a grade for it.

3. Lectures on some metatheory

Then Herman will use the next three weeks to teach part of:

Herman Geuvers, Introduction to Type Theory

using the schedule:

15 October	principal types and type checking	sections 4.1-4.3, 6.4 slides, exercises, answers
19 October	Church-Rosser property	section 3.1 slides, exercises, answers
9 November	normalization of λ→ and λ2	sections 4.4, 5.6 slides, exercises, answers

This concludes the first half of the course.

4. Exam

The exam will not be at the end of the course but halfway through. Therefore the subject of the exam will be just the lectures by Freek and Herman, and not the topic of the reading group.

The date of the exam will be:

19 November

two hour exam on the theory in HG00.307

See at the end of this web page for some material to practise for the exam, like old exams from last years.

5. Reading group with presentations

In the second half of the course we read about recent research. The topic of the papers this year is the Lean system.

The presentations are by the students in pairs. These presentations are 45 minutes, and should contain both examples, as well as the gist of the proofs in the paper. It is more important to explain the important points of the paper well, then to cover everything in full detail.

The papers for this year, together with the students that will present them, are:

Jeremy Avigad, Leonardo de Moura, Soonho Kong, Theorem Proving in Lean (manual), Oct 02, 2021.
1. Section 5–6 + Lean demo in VS Code
  Suzan Erven & Amber Pater: 30 November
2. Section 11: classical axioms (see also The Type Theory of Lean, Section 2.7)
  Menno Bartels & Roy Willems: 3 December

Mario Carneiro, The Type Theory of Lean. 2019.
1. Section 2: typing rules
  Jeroen van Wees: 3 December
2. Sections 3–4: undecidability of conversion
  Wietze Koops & Niels Vooijs: 7 December
3. Section 5: W types
  Bálint Kocsis & Márk Széles: 7 December
4. Section 6: ZFC model
  Thijs van Loenhout & Sander Suverkropp: 10 December

Gabriel Ebner, Sebastian Ullrich, Jared Roesch, Jeremy Avigad, Leonardo de Moura, A metaprogramming framework for formal verification. PACMPL, 2017.
Markel Zubia: 10 December
Alex Reinking, Ningning Xie, Leonardo de Moura, Daan Leijen, Perceus: Garbage Free Reference Counting with Reuse, PLDI 2021: Programming Language Design and Implementation.
Kirsten Hagenaars & Astrid van der Jagt: 14 December
Daniel Selsam, Simon Hudon, Leonardo de Moura, Sealing Pointer-Based Optimizations behind Pure Functions. Proc. ACM Program. Lang., 2020.
Buster Bosma & Michiel Philipse: 14 December
Daniel Selsam, Sebastian Ullrich, Leonardo de Moura, Tabled Typeclass Resolution. 2020.
Dor Alter & Orpheas van Rooij: 17 December
Sebastian Ullrich, Leonardo de Moura, Beyond Notations: Hygienic Macro Expansion for Theorem Proving Languages. Automated Reasoning - 10th International Joint Conference, IJCAR 2020, Paris, France, July 1–4, 2020, Proceedings, Part II, 2020.
(not assigned)
The mathlib community, The Lean mathematical library. Proceedings of the 9th ACM SIGPLAN International Conference on Certified Programs and Proofs, CPP 2020, New Orleans, LA, USA, January 20–21, 2020, 2020.
Stijn van den Beemt & Willem Lambooij: 17 December
Eric Wieser, Scalar actions in Lean's mathlib. 2021.
Steven Bronsveld & Jelmer Firet: 21 December
Mario Carneiro, Porting Mathlib (talk), Formal Mathematics for Mathematicians (FMM) 2021.
(not assigned)
Mario Carneiro, Formalizing Computability Theory via Partial Recursive Functions. 10th International Conference on Interactive Theorem Proving, ITP 2019, September 9–12, 2019, Portland, OR, USA, 2019.
Robin Holen & Mirja van de Pol: 21 December

So the schedule for the presentations is:

30 November	Lean demo	Suzan Erven & Amber Pater slides
3 December	classical axioms	Menno Bartels & Roy Willems slides
	typing rules	Jeroen van Wees slides slides
7 December	undecidability	Wietze Koops & Niels Vooijs slides
	W types	Bálint Kocsis & Márk Széles slides lean
10 December	ZFC model	Thijs van Loenhout & Sander Suverkropp slides
	metaprogramming	Markel Zubia slides
14 December	reference counting	Kirsten Hagenaars & Astrid van der Jagt slides
	pointers	Buster Bosma & Michiel Philipse slides
17 December	typeclass resolution	Dor Alter & Orpheas van Rooij slides
	Mathlib	Stijn van den Beemt & Willem Lambooij slides
21 December	scalar actions	Steven Bronsveld & Jelmer Firet slides
	computability theory	Robin Holen & Mirja van de Pol slides

6. Coq project

Each student has to do a small Coq project. This project can be chosen from

list of possible projects

but if students have a suggestion for an interesting project that they want to do, that is also allowed.

The deadline for the Coq project is 19 January 2022.

Grading

You will get three marks: for the exam, the Coq presentations, and the Coq project (items 4, 5 and 6 above). The final mark for the course is the average of those three marks, rounded to a half integral number. A mark of 5.5 will be rounded up to 6, and the mark for the exam has to be at least 5.0.

IMC010: Type Theory and Coq

Teachers

Structure of the course

1. Lectures on using type theory

2. Coq practicum

3. Lectures on some metatheory

4. Exam

5. Reading group with presentations

6. Coq project

Grading

Some supporting material

Coq support from Jules

Paper exercises

Old exams

Some slides