IMC010: Type Theory and Coq

Teachers

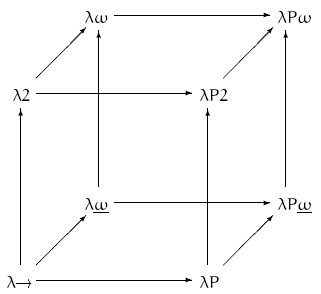
Structure of the course

The course consists of six parts:

1. Lectures on the type theory of Coq

Freek will use the first five weeks to teach part of:

Femke van Raamsdonk, Logical Verification Course Notes

using the schedule:

6 September	introduction & lambda calculus
13 September	propositional logic & simple types	chapters 1 & 2
20 September	predicate logic & dependent types	chapters 4 & 6
27 September	inductive types & inductive predicates	chapter 3
4 October	second-order logic & polymorphic types	chapters 7 & 8

2. Coq practicum

There will be a Coq practicum corresponding to Femke's course notes. For this you need to install Coq and download a

zip file with the practicum files

The completed files need to be handed in in Brightspace. Finishing this practicum is obligatory to be able to pass the course, but there will not be a grade for it.

3. Lectures on some metatheory

Then Herman will use the next three weeks to teach part of:

Herman Geuvers, Introduction to Type Theory

using the schedule:

11 October	principal types & type checking	sections 4.1-4.3, 6.4 slides, exercises, answers
18 October	Church-Rosser property	section 3.1 slides, exercises, answers
8 November	normalization of λ→ and λ2	sections 4.4, 5.6 slides, exercises, answers

This concludes the first half of the course.

4. Exam

The exam will not be at the end of the course but halfway through. Therefore the subject of the exam will be just the lectures by Freek and Herman, and not the topic of the reading group.

The date of the exam will be:

16 November

two hour exam on the theory in E 2.50

See at the end of this web page for some material to practise for the exam, like old exams from last years.

5. Reading group with presentations

In the second half of the course we read papers about a specific topic related to a recent research publication (a different topic every year). The topic of this year will be cubical type theory.

The presentations are by the students in pairs. These presentations are 45 minutes, and should contain both examples, as well as the gist of the proofs in the paper. It is more important to explain the important points of the paper well, then to cover everything in full detail.

The book and papers for this year, together with the students that will present them, are:

The Univalent Foundations Program, Homotopy Type Theory, Univalent Foundations of Mathematics, 2003.
1. Sections 2.1–2.3 (important: path induction)
  Aron Schöffer & Tjitske Koster: 30 november
2. Sections 2.4–2.8 (important: notion of equivalence, higher groupoids)
  Gé Waayers & Nick Hendriks: 30 november
3. Sections 2.9–2.12 (important: universes and univalence)
  Niels van der Weide: 6 december
4. Sections 2.13–2.15 (important: 2.14, application of univalence)
  Daniël van Leijenhorst & Finn van der Velde: 6 december
5. Sections 3.1–3.4, 3.6, 3.7 (important: h-levels and truncation)
  Niek Terol & Thomas Somers: 7 december
6. Sections 6.9–6.11 (important: examples of HITs)
  David Läwen & Jakob Wuhrer: 7 december

Cyril Cohen, Thierry Coquand, Simon Huber, Anders Mörtberg, Cubical Type Theory: a constructive interpretation of the univalence axiom, 2016.
1. Section 2–3 (important: what are path types?)
  Bryan van de Ven & Cas Visser: 13 december
2. Sections 4–5 (important: operations on paths)
  Daan Spijkers & Samuel Klumpers: 13 december
3. Section 6–7 (important: what are glue types and how does univalence follow from that?)
  Mika van Emmerloot & Marten Straatsma: 14 december

Ana Bove, Peter Dybjer, Ulf Norell, A Brief Overview of Agda – A Functional Language with Dependent Types, 2009.
1. Full paper + demo (important: how to use Agda?)
  Alwyn Stiles & Eef Uijen: 14 december

Andrea Vezzosi, Anders Mörtberg, Andreas Abel, Cubical Agda: A Dependently Typed Programming Language with Univalence and Higher Inductive Types, 2020.
1. Sections 2.1, 2.2, 2.4, 2.5 + demo (important: how to use Cubical Agda?)
  Dante van Gemert & Paul Tiemeijer: 20 december

Carlo Angiuli, Evan Cavallo, Anders Mörtberg, Max Zeuner, Internalizing Representation Independence with Univalence, 2020.
1. Sections 2 (important: notation and set-up of the paper)
  Aron van Hof & Bram Pellen: 20 december
2. Sections 3 (important: what is the structure identity principle?)
  Gerbrich Kroon & Rutger Dinnissen: 21 december
3. Sections 4–5 (important: how to use that principe?)
  Alex van der Hulst & Simcha van Collem: 21 december

So the schedule for the presentations is:

30 November	path induction	Aron Schöffer & Tjitske Koster slides
	equivalence, higher groupoids	Gé Waayers & Nick Hendriks slides
6 December	universes, univalence	Niels van der Weide slides
	application of univalence	Daniël van Leijenhorst & Finn van der Velde slides
7 December	h-levels, truncation	Niek Terol & Thomas Somers slides
	examples of HITs	David Läwen & Jakob Wuhrer slides
13 December	path types	Bryan van de Ven & Cas Visser slides
	operations on paths	Daan Spijkers & Samuel Klumpers slides
14 December	glue types	Mika van Emmerloot & Marten Straatsma slides
	Agda	Alwyn Stiles & Eef Uijen slides sources
20 December	Cubical Agda	Dante van Gemert & Paul Tiemeijer slides
	the paper	Aron van Hof & Bram Pellen slides
21 December	structure identity principle	Gerbrich Kroon & Rutger Dinnissen slides
	using the principle	Alex van der Hulst & Simcha van Collem slides

6. Coq project

Each student has to do a small Coq project. This project can be chosen from

list of possible projects

but if students have a suggestion for an interesting project that they want to do, that is also allowed.

The deadline for the Coq project is 20 January 2023.

Grading

You will get three marks: for the exam, the Coq presentations, and the Coq project (items 4, 5 and 6 above). The final mark for the course is the average of those three marks, rounded to a half integral number. A mark of 5.5 will be rounded up to 6, and the mark for the exam has to be at least 5.0.

IMC010: Type Theory and Coq

Teachers

Structure of the course

1. Lectures on the type theory of Coq

2. Coq practicum

3. Lectures on some metatheory

4. Exam

5. Reading group with presentations

6. Coq project

Grading

Some supporting material

Supporting documents

Paper exercises

Old exams

Some slides